在七年級上學期一定會上到指數律,而上到指數律的時候會掰一個故事,每次說的版本都會有所不同,不過,這頗具深義的小故事,我大概是這樣說的:
有一天,有一位掌管幸福的仙女不慎落入森林,失去了法力,在野獸環伺的危及時刻,一個平凡的獵人路過,勇敢地伸出援手,將仙女從猛獸的口中救回,並細心照料仙女的傷勢,直到她又恢復了法力,有貌似天仙的光采。
然而,仙女必須回到在天上的工作崗位,但感念於獵人的恩情與照顧,臨走前,想給老實的獵人一點獎賞,順便測試獵人的人性,看他是否只是因為自己的美貌才如此,還是真的是一個善良、不貪心的獵人;於是仙女給獵人兩個獎賞做選擇...選擇:「第一天給你1塊錢,第二天開始,隔天我會給你前一天的錢的加倍,直到一個月結束」;選擇二:「從第一天開始,每天不間斷的,都給你一千萬,也將持續一個月」。
善良的獵人覺得救人是應該的,也不貪求財富,所以選擇了第一個方案。
故事到此,我會問學生:「那麼你選什麼?」##ReadMore##
絕大多數的學生,想都不想就「當然」選擇了方案二,這也無可厚非,在經濟不景氣的現代,故事中「善良的獵人」是幾乎已經滅絕的生物;然而,若再提醒學生:「每天都加倍喔!」、「要不要用剛剛教過的指數律試著算算看?」;學生便會開始猶豫、開始動筆計算,但過不了多久,90%就是放棄計算之後仍然堅持方案二的選擇,因為這時,通常只是第一節課的引導活動,孩子只會、也只能,2*2*2*2*2*2.....慢慢的乘,再慢慢的加總;一個月30天就夠他們算的了。
把這問題丟給大人,就會比較有趣些,因為大人更懂得「揣測」,雖然覺得30天一千萬很多,但也不免懷疑方案一是否真的會超過三億?!如果要避免被「揣測」到,教你一招,你可以把故事中選擇二的每天金額,先降低改成一百萬,等有人自信滿滿的回答「當然選方案一啊!」的時候,你再將選擇二的金額一口氣提高10倍變成一千萬,很多人便會開始猶豫了。
那麼,來看看實際的金額到底是多少吧:
| 第幾天 | 方案一所獲得金額 | 方案二所獲得金額 | 兩者差額 |
| 1 | 1 | 10000000 | -9999999 |
| 2 | 2 | 10000000 | -9999998 |
| 3 | 4 | 10000000 | -9999996 |
| 4 | 8 | 10000000 | -9999992 |
| 5 | 16 | 10000000 | -9999984 |
| 6 | 32 | 10000000 | -9999968 |
| 7 | 64 | 10000000 | -9999936 |
| 8 | 128 | 10000000 | -9999872 |
| 9 | 256 | 10000000 | -9999744 |
| 10 | 512 | 10000000 | -9999488 |
| 11 | 1024 | 10000000 | -9998976 |
| 12 | 2048 | 10000000 | -9999752 |
| 13 | 4096 | 10000000 | -9995904 |
| 14 | 8192 | 10000000 | -9991808 |
| 15 | 16384 | 10000000 | -9983616 |
| 16 | 32768 | 10000000 | -9967232 |
| 17 | 65536 | 10000000 | -9934464 |
| 18 | 131072 | 10000000 | -9868928 |
| 19 | 262144 | 10000000 | -9737856 |
| 20 | 524288 | 10000000 | -9475712 |
| 21 | 1048576 | 10000000 | -8951424 |
| 22 | 2097152 | 10000000 | -7902848 |
| 23 | 4194304 | 10000000 | -5805696 |
| 24 | 8388608 | 10000000 | -1611392 |
| 25 | 16777216 | 10000000 | +6777216 |
| 26 | 33554432 | 10000000 | +23554432 |
| 27 | 67108864 | 10000000 | +57108864 |
| 28 | 134217728 | 10000000 | +124217728 |
| 29 | 268435456 | 10000000 | +258435456 |
| 30 | 536870912 | 10000000 | +526870912 |
| 金額總和 | 1073741823 | 300000000 | +773741823 |
由上面的表格可以看得出來,第24天方案一還落後方案二160幾萬;但到了第25天,卻一下子超前677萬多;第26天的領先更是一口氣達到2355萬;越到後面,加倍的威力更加強大,光是月底第30天這一天,方案一就贏了方案二5億多元,雖然1~24天都輸,但累積30天的金額加總,還是贏了7.7億!
看以下的圖表,也許你會更能體會那樣的差距感:
ps. X軸的31表示1~30天的加總
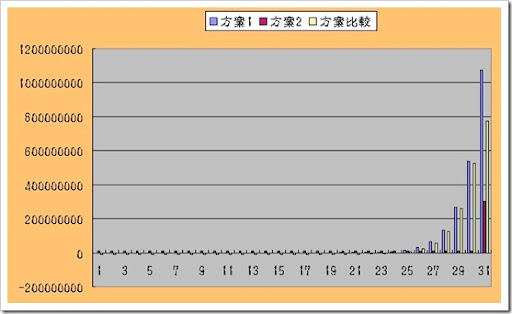
5億是1000萬的50倍大!
有沒有發現,1000萬的微不足道,我簡直快看不到方案二的長條圖顏色了。
當我把確實的數據算給孩子看的時候,每個人的驚訝,都寫在張得大大嘴巴與呆滯的表情上;等回過神來之後,愛哈啦的同學會問說:「老師,那你會選哪個?」
我說:「選一千萬感覺是個貪心的人;但身為數學老師,明明知道選擇一等於10億多,如果選了,不就代表是個更貪心的人嗎?」所以該怎麼辦才好呢?
「那我只好勉為其難的選仙女了吧!下課....」
















7 留下回應:
這個故事很有意思~
謝謝:)
這故事真有趣!下星期一要幫學生們上指數律,上網找指數律有關的活動(上次找不到適合的),今天上來正好發現這篇文章,真的很有意思。
如果您還有其它有趣好玩的實際活動(可讓學生們真正動起來的)也能大方分享。謝謝您了^^!
呵呵,有想到什麼活動,有時間我都會把它寫上來分享的^_^
我是即將升國中的學生!
謝謝你的故事讓我更了解指數律!
不過還是不太會算耶!
有個"網路兼職"機會替自己加薪,增加存款!
給自己一個機會深入瞭解吧!
免費索取在家網路兼職資料 。
http://joe80411.weebly.com/
祝~天天都是有美好的一天˙快樂與您同在
PS:謝謝您的閱讀。如果您不感興趣,很抱歉打擾您!!
這篇故事還滿有趣的:)
讓我更了解指數律囉:)
謝謝提供:)
張貼留言
別再潛水囉,快透出水面透透氣吧!
沒有Blogger帳號的朋友,請選[名稱/網址],然後留下部落格網址,
讓我知道你來自哪裡喔 :)